Code
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import xgboost as xgb
plt.rcParams['figure.figsize'] = (7, 7)kakamana
January 21, 2023
After a brief review of supervised regression, you’ll apply XGBoost to the regression task of predicting house prices in Ames, Iowa. Aside from learning how XGboost can evaluate the quality of your regression models, you will also learn about the two types of base learners it can use as weak learners.
This Regression with XGBoost is part of Datacamp course: Extreme Gradient Boosting with XGBoost
This is my learning experience of data science through DataCamp


It’s now time to build an XGBoost model to predict house prices - not in Boston, Massachusetts, as you saw in the video, but in Ames, Iowa! This dataset of housing prices has been pre-loaded into a DataFrame called df. If you explore it in the Shell, you’ll see that there are a variety of features about the house and its location in the city.
In this exercise, your goal is to use trees as base learners. By default, XGBoost uses trees as base learners, so you don’t have to specify that you want to use trees here with booster="gbtree".
Note:
reg:linearis replaced withreg:squarederror
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1460 entries, 0 to 1459
Data columns (total 57 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 MSSubClass 1460 non-null int64
1 LotFrontage 1460 non-null float64
2 LotArea 1460 non-null int64
3 OverallQual 1460 non-null int64
4 OverallCond 1460 non-null int64
5 YearBuilt 1460 non-null int64
6 Remodeled 1460 non-null int64
7 GrLivArea 1460 non-null int64
8 BsmtFullBath 1460 non-null int64
9 BsmtHalfBath 1460 non-null int64
10 FullBath 1460 non-null int64
11 HalfBath 1460 non-null int64
12 BedroomAbvGr 1460 non-null int64
13 Fireplaces 1460 non-null int64
14 GarageArea 1460 non-null int64
15 MSZoning_FV 1460 non-null int64
16 MSZoning_RH 1460 non-null int64
17 MSZoning_RL 1460 non-null int64
18 MSZoning_RM 1460 non-null int64
19 Neighborhood_Blueste 1460 non-null int64
20 Neighborhood_BrDale 1460 non-null int64
21 Neighborhood_BrkSide 1460 non-null int64
22 Neighborhood_ClearCr 1460 non-null int64
23 Neighborhood_CollgCr 1460 non-null int64
24 Neighborhood_Crawfor 1460 non-null int64
25 Neighborhood_Edwards 1460 non-null int64
26 Neighborhood_Gilbert 1460 non-null int64
27 Neighborhood_IDOTRR 1460 non-null int64
28 Neighborhood_MeadowV 1460 non-null int64
29 Neighborhood_Mitchel 1460 non-null int64
30 Neighborhood_NAmes 1460 non-null int64
31 Neighborhood_NPkVill 1460 non-null int64
32 Neighborhood_NWAmes 1460 non-null int64
33 Neighborhood_NoRidge 1460 non-null int64
34 Neighborhood_NridgHt 1460 non-null int64
35 Neighborhood_OldTown 1460 non-null int64
36 Neighborhood_SWISU 1460 non-null int64
37 Neighborhood_Sawyer 1460 non-null int64
38 Neighborhood_SawyerW 1460 non-null int64
39 Neighborhood_Somerst 1460 non-null int64
40 Neighborhood_StoneBr 1460 non-null int64
41 Neighborhood_Timber 1460 non-null int64
42 Neighborhood_Veenker 1460 non-null int64
43 BldgType_2fmCon 1460 non-null int64
44 BldgType_Duplex 1460 non-null int64
45 BldgType_Twnhs 1460 non-null int64
46 BldgType_TwnhsE 1460 non-null int64
47 HouseStyle_1.5Unf 1460 non-null int64
48 HouseStyle_1Story 1460 non-null int64
49 HouseStyle_2.5Fin 1460 non-null int64
50 HouseStyle_2.5Unf 1460 non-null int64
51 HouseStyle_2Story 1460 non-null int64
52 HouseStyle_SFoyer 1460 non-null int64
53 HouseStyle_SLvl 1460 non-null int64
54 PavedDrive_P 1460 non-null int64
55 PavedDrive_Y 1460 non-null int64
56 SalePrice 1460 non-null int64
dtypes: float64(1), int64(56)
memory usage: 650.3 KBfrom sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# Create the training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=123)
# Instantiatethe XGBRegressor: xg_reg
xg_reg = xgb.XGBRegressor(objective='reg:squarederror', seed=123, n_estimators=10)
# Fit the regressor to the training set
xg_reg.fit(X_train, y_train)
# Predict the labels of the test set: preds
preds = xg_reg.predict(X_test)
# compute the rmse: rmse
rmse = np.sqrt(mean_squared_error(y_test, preds))
print("RMSE: %f" % (rmse))
print("Next, you'll train an XGBoost model using linear base learners and XGBoost's learning API. Will it perform better or worse?")RMSE: 28106.463641
Next, you'll train an XGBoost model using linear base learners and XGBoost's learning API. Will it perform better or worse?Now that you’ve used trees as base models in XGBoost, let’s use the other kind of base model that can be used with XGBoost - a linear learner. This model, although not as commonly used in XGBoost, allows you to create a regularized linear regression using XGBoost’s powerful learning API. However, because it’s uncommon, you have to use XGBoost’s own non-scikit-learn compatible functions to build the model, such as xgb.train().
In order to do this you must create the parameter dictionary that describes the kind of booster you want to use (similarly to how you created the dictionary in Chapter 1 when you used xgb.cv()). The key-value pair that defines the booster type (base model) you need is "booster":"gblinear".
Once you’ve created the model, you can use the .train() and .predict() methods of the model just like you’ve done in the past.
# Convert the training and testing sets into DMatrixes: DM_train, DM_test
DM_train = xgb.DMatrix(data=X_train, label=y_train)
DM_test = xgb.DMatrix(data=X_test, label=y_test)
# Create the parameter dictionary: params
params = {"booster":"gblinear", "objective":"reg:squarederror"}
# Train the model: xg_reg
xg_reg = xgb.train(params=params, dtrain=DM_train, num_boost_round=5)
# Predict the labels of the test set: preds
preds = xg_reg.predict(DM_test)
# Compute and print the RMSE
rmse = np.sqrt(mean_squared_error(y_test, preds))
print("RMSE: %f" % (rmse))
print("\nit looks like linear base learners performed better!")RMSE: 44305.046080
it looks like linear base learners performed better!It’s now time to begin evaluating model quality.
Here, you will compare the RMSE and MAE of a cross-validated XGBoost model on the Ames housing data.
# Create the DMatrix: housing_dmatrix
housing_dmatrix = xgb.DMatrix(data=X, label=y)
# Create the parameter dictionary: params
params = {"objective":"reg:squarederror", "max_depth":4}
# Perform cross-valdiation: cv_results
cv_results = xgb.cv(dtrain=housing_dmatrix, params=params, nfold=4,
num_boost_round=5, metrics='rmse', as_pandas=True, seed=123)
# Print cv_results
print(cv_results)
# Extract and print final boosting round metric
print((cv_results['test-rmse-mean']).tail(1)) train-rmse-mean train-rmse-std test-rmse-mean test-rmse-std
0 141767.533478 429.451090 142980.434934 1193.795492
1 102832.547530 322.472076 104891.395389 1223.157368
2 75872.617039 266.474211 79478.938743 1601.345019
3 57245.651780 273.624239 62411.921348 2220.150063
4 44401.298519 316.423620 51348.279619 2963.378136
4 51348.279619
Name: test-rmse-mean, dtype: float64# Create the DMatrix: housing_dmatrix
housing_dmatrix = xgb.DMatrix(data=X, label=y)
# Create the parameter dictionary: params
params = {"objective":"reg:squarederror", "max_depth":4}
# Perform cross-valdiation: cv_results
cv_results = xgb.cv(dtrain=housing_dmatrix, params=params, nfold=4,
num_boost_round=5, metrics='mae', as_pandas=True, seed=123)
# Print cv_results
print(cv_results)
# Extract and print final boosting round metric
print((cv_results['test-mae-mean']).tail(1)) train-mae-mean train-mae-std test-mae-mean test-mae-std
0 127343.480012 668.306786 127633.999275 2404.005913
1 89770.056424 456.963854 90122.501070 2107.909841
2 63580.789280 263.405054 64278.558741 1887.567534
3 45633.156501 151.883868 46819.168555 1459.818435
4 33587.090044 86.998100 35670.647207 1140.607311
4 35670.647207
Name: test-mae-mean, dtype: float64Having seen an example of l1 regularization in the video, you’ll now vary the l2 regularization penalty - also known as "lambda" - and see its effect on overall model performance on the Ames housing dataset.
# Create the DMatrix: housing_dmatrix
housing_dmatrix = xgb.DMatrix(data=X, label=y)
reg_params = [1, 10, 100]
# Create the initial parameter dictionary for varying l2 strength: params
params = {"objective":"reg:squarederror", "max_depth":3}
# Create an empty list for storing rmses as a function of l2 complexity
rmses_l2 = []
# Iterate over reg_params
for reg in reg_params:
# Update l2 strength
params['lambda'] = reg
# Pass this updated param dictionary into cv
cv_results_rmse = xgb.cv(dtrain=housing_dmatrix, params=params, nfold=2,
num_boost_round=5, metrics='rmse', as_pandas=True, seed=123)
# Append best rmse (final round) to rmses_l2
rmses_l2.append(cv_results_rmse['test-rmse-mean'].tail(1).values[0])
# Loot at best rmse per l2 param
print("Best rmse as a function of l2:")
print(pd.DataFrame(list(zip(reg_params, rmses_l2)), columns=["l2", "rmse"]))
print("\nIt looks like as as the value of 'lambda' increases, so does the RMSE.")Best rmse as a function of l2:
l2 rmse
0 1 52275.357003
1 10 57746.063828
2 100 76624.627811
It looks like as as the value of 'lambda' increases, so does the RMSE.Now that you’ve used XGBoost to both build and evaluate regression as well as classification models, you should get a handle on how to visually explore your models. Here, you will visualize individual trees from the fully boosted model that XGBoost creates using the entire housing dataset.
XGBoost has a plot_tree() function that makes this type of visualization easy. Once you train a model using the XGBoost learning API, you can pass it to the plot_tree() function along with the number of trees you want to plot using the num_trees argument.
# Create the DMatrix: housing_dmatrix
housing_dmatrix = xgb.DMatrix(data=X, label=y)
# Create the parameters dictionary: params
params = {"objective":'reg:squarederror', 'max_depth':2}
# Train the model: xg_reg
xg_reg = xgb.train(dtrain=housing_dmatrix, params=params, num_boost_round=10)
# Plot the first tree
fig, ax = plt.subplots(figsize=(15, 15))
xgb.plot_tree(xg_reg, num_trees=0, ax=ax);
# Plot the fifth tree
fig, ax = plt.subplots(figsize=(15, 15))
xgb.plot_tree(xg_reg, num_trees=4, ax=ax);
# Plot the last tree sideways
fig, ax = plt.subplots(figsize=(15, 15))
xgb.plot_tree(xg_reg, rankdir="LR", num_trees=9, ax=ax);
print("\nHave a look at each of the plots. They provide insight into how the model arrived at its final decisions and what splits it made to arrive at those decisions. This allows us to identify which features are the most important in determining house price. In the next exercise, you'll learn another way of visualizing feature importances.")ExecutableNotFound: failed to execute WindowsPath('dot'), make sure the Graphviz executables are on your systems' PATH
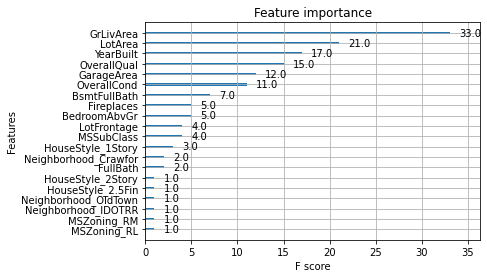
Another way to visualize your XGBoost models is to examine the importance of each feature column in the original dataset within the model.
One simple way of doing this involves counting the number of times each feature is split on across all boosting rounds (trees) in the model, and then visualizing the result as a bar graph, with the features ordered according to how many times they appear. XGBoost has a plot_importance() function that allows you to do exactly this, and you’ll get a chance to use it in this exercise!
# Create the DMatrix: housing_dmatrix
housing_dmatrix = xgb.DMatrix(data=X, label=y)
# Create the parameter dictionary: params
params = {"objective":"reg:squarederror", "max_depth":4}
# Train the model: xg_reg
xg_reg = xgb.train(dtrain=housing_dmatrix, params=params, num_boost_round=10)
# Plot the feature importance
xgb.plot_importance(xg_reg);